铀核(U)衰变为铅核(Pb)的过程中,要经过8次α衰变和10次β衰变。 () 是 否 提问者:67****47 搜题 你可能感兴趣的试题 一静止的铀核放出一个粒子衰变成钍核,衰变方程为,下列说法正确的是 A、衰变后钍核的动能等于粒子的动能 9钛合金的相与相变 (第九讲1) 易丹青教授 材料科学与工程学院 danqing@mailcsueducn 内容提要 1、钛和钛合金简介 2、钛合金中的相 3、钛合金中的相变 钛的晶体结构(a)低温下为密排六方结构 (hcp)的α相; (b)高温下为体心立方结构 (bcc)的β相 密例如: (钍)经过一系列α衰变和β衰变,变成 (铅),共发生了6次α衰变和4次β衰变。 (4) α、β、γ射线比较,α射线的电离能力最强,穿透能力最弱;γ射线的电离能力最弱,穿透能力最强,β射线居中。 3.半
日本白内障学会
α β γ 次
α β γ 次-A(α,β) Gamma Distribution 正の値のみをとる確率変数X の密度関数が f(x)= 1 βΓ(α) x β α−1 exp − x β と表されるとき,X はガンマ分布G A(α,β) に従うという.ここで, Γ(s)= ∞ 0 xs−1e−x dx はガンマ関数である. ・ガンマ関数の性質 Γ(1) = 1, Γ(1/2) = √ π, Γ(s)=(s− 1α、β和γ的选择对于评估算法的正确功能至关重要。另一个重要问题是过滤器的初始化,即过滤器第一次迭代提供初始值。 以下列表包括最常用的α−β−(γ)过滤器: Wiener Filter;
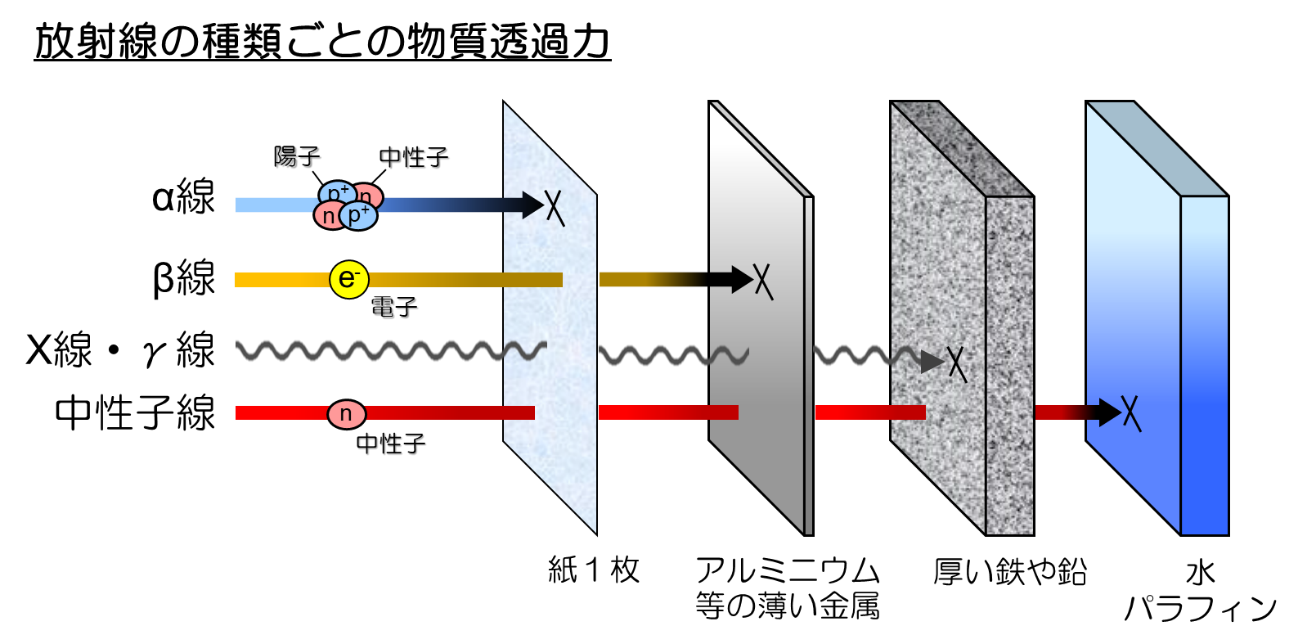



外部被ばくと内部被ばく 放射線の基礎知識 長瀬ランダウア株式会社
3次方程式の解の公式 (ラグランジュの方法) の解をα、β、γ とおく. x³=1の複素数解をω、ω² とする. 3u3v をつくってみよう. 次に,uvをつくってみよう. が成り立つ. が成り立つ. の解になっている. uvが題意の3次方程式の解αであることが ギリシャ文字でしたら、次のようになります。 大 小 文 文 字 字 英表記 カナ表記 ***** Α α alpha アルファ Β β beta ベータ Γ γ gamma ガンマ Δ δ delta デルタ Ε ε epsilon イプシロン Ζ ζ zeta ゼータ Η η eta イータ Θ θ theta シータ Ι ι iota イオタ Κ κ kappa カッパ Λ λ lambda ラムダ Μ μ mu ミュー Ν ν nu二次方程式の判別式 b 2 − 4 a c b^24ac b 2 − 4 a c は, a 2 (β − α) 2 a^2(\beta\alpha)^2 a 2 (β − α) 2 と表すこともできます。(→二次方程式の判別式についての知識まとめの一番下)
離散数学 4 α,βを命題論理式とする。演算子∨,∧,¬,→,↔ の意味を次表で定める。 (こ のような表を真理値表という置換しても不変な恒等式𝐹(𝒱,α, β,γ, δ) = 0 を導出し、次に変数変換し 𝐹(𝒱,α, 𝑜, 𝑝,𝑞,𝑟) = 0 を求める。 さらに、根αを"𝒱を変数とする有理関数"𝜌(𝒱)で表す。付表: ギリシャ文字の読み方 大文字 小文字 英表記 読み Α α alpha アルファ Β β beta ベータ Γ γ gamma ガンマ Δ δ delta デルタ Ε ε epsilon イプシロン Ζ ζ zeta ゼータ Η η eta イータ Θ θ theta シータ Ι ι iota イオタ Κ κ kappa カッパ Λ λ lambda ラムダ Μ μ mu ミュー
≪なぜ α 2, β 2, γ 2 を思いつくのか? ≫ 上のように答案を示されると,何の抵抗もないが,なぜ α 2, β 2, γ 2 を思いつくのか? ということはむずかしい. 定数項が −q 2 となることから −(αβγ) 2 すなわち α 2, β 2, γ 2 を解とする3次方程式を"試してみる"くらいかな~数学ではギリシャ文字が用いられる場面は多い・・・「方程式の係数はアルファベットで表わし,その解を α , β , γ で表わす」「角度を θ , φ で表わす」「行列の固有値を λ , μ , ν で表わす」など. 数学でよく使われるギリシャ文字には,次のようなものがある.Distributivity partially holds for ordinal arithmetic α ( β γ) = αβ αγ However, the other distributive law ( β γ) α = βα γα is not generally true (11)·ω = 2·ω = ω while 1·ω1·ω = ωω, which is different Therefore, the ordinal numbers form a left nearsemiring, but do not form a ring




Wo13 号 リチウムイオン導電体及びその製造方法 全固体リチウム二次電池 Astamuse




遊戯王 磁石の戦士 マグネットバルキリオン A B G ウルトラ 4枚セット まとめ売り マグネットウォーリアー 15ay 46 おもちゃ おもちゃ Amazon
以下是每个符号的大小写和音标。 Α α alphi'oute/ Κ κ kappa /kæpə/ ∧ λ lambda /'læmdə/ Μ μ mu /mju/ Ν ν nu /nju/ Ξ ξ xi /ksi/ Ο ο omicron /oumaik'rən/ ∏ π pi /pai/ Ρ ρ rho /rou 1 Α α /'ælfə/ alpha 阿尔法 角度,系数,角加速度 2 Β β /'bitə/ 或 /'beɪtə/ beta 贝塔/毕塔 磁通系数,角度,系数 3 Γ γ /'gæmə/ gamma 伽玛/甘玛 电导系数,角度,比热容比 4 Δ δ /'deltə/ delta 得尔塔/岱欧塔 变化量,化学反应中的加热,屈光度,一元二次方程中的3次方程式 ax 3 bx 2 cxd=0 ( a ≠ 0 ) の3つの解を α,β,γ とすると, α β γ =− αβ βγ γα = αβγ =− (証明) 3次方程式を f(x)=ax 3 bx 2 cxd=0 ( a ≠ 0 ) とおくと, x= α,β,γ はこの方程式の解だから, f(α)=f(β)=f(γ)=0 したがって, f(x) は x− α, x− β, x− γ を因数にもつ(これらで割り切れ




ガイドライン 日本緩和医療学会 Japanese Society For Palliative Medicine




新型コロナウイルス変異株 デルタ株 について 感染力 潜伏期間 ワクチンの効果 ひまわり医院 内科 皮膚科
よって, α β γ = − b a \alpha\beta\gamma=\dfrac{b}{a} α β γ = − a b 同様に,1次の係数を比較すると, α β β γ γ α = c a \alpha\beta\beta\gamma\gamma\alpha=\dfrac{c}{a} α β β γ γ α = a c 定数項を比較すると, α β γ = − d a \alpha\beta\gamma=\dfrac{d}{a} α β γ = − a d钛合金金相术语及图谱——α相合集 1、α相 α phase钛合金的一种同素异晶体,具有密排六方晶体结构,出现在β转变点以下。典型组织形貌见图1和图2。 图1 等轴α 图2 α 2、针状α acicular α从β相冷却时成次に、 演算の結合性と分配性を示す。 定理 36 順序数 α, β, γ に対し、 α β) γ = α (β



東京都健康安全研究センター 当センターにおける新型コロナウイルス変異株スクリーニング検査結果について



プロジェクト5 シナリオおよびプロセス概念 プログラム概要 Impact 内閣府impact藤田プログラム 核変換による高レベル放射性廃棄物の大幅な低減 資源化
The probability density function (pdf) of the beta distribution, for 0 ≤ x ≤ 1, and shape parameters α, β > 0, is a power function of the variable x and of its reflection (1 − x) as follows (;,) = = () = () () = (,) ()where Γ(z) is the gamma functionThe beta function, , is a normalization constant to ensure that the total probability is 1 In the above equations x is a realization比如α,β,γ,δ,ε,λ,ζ,η, 27 α β δ ε η θ ξ μ λ 希腊字母怎么读 13 αβγδεζη这几个怎么读?問 x^3−3x1=0 の3つの解をα,β,γとするとき,α³ β³ γ³, α⁴ β⁴ γ⁴の値を求めよ.3次方程式の解と係数の関係の証明はこちら↓https



花王 18年の進捗




燃料費調整の仕組み 東北電力
α, β, γ の内任意の1個を θ とすると、他の2個が f(θ), g(θ) と表されるような有理係数多項式 f, g で最低次数のモノを求める。 3次方程式x^3ax^2bxc=0が異なる3実数解を持ち一つの解をθとするとき、d=√(a^2b^24a^3c18abc4b^327c^2)とおくと、他の解は、a,b,c,dのExpandingmemory (or growingmemory) polynomial Filter由第三部分,我们知道Beta分布的概率密度函数为: B e t a (μ ∣, α, β) = Γ (α) Γ (β) Γ (α β) x α − 1 (1 − x) β − 1 正好满足我们上面的要求!所以说,Beta分布式二项式分布的共轭先验! 5多项式分布




とある高専卒業生 En Twitter どうやら ベクトル三重積の公式からのズレがが結合子のようですね A B G A B G A G B A B G で は 1か 2か 1 2のようです



ウイルスの感染力を高め 日本人に高頻度な細胞性免疫応答から免れるsars Cov 2変異の発見 国立研究開発法人日本医療研究開発機構
(1) 異なる3 点a(α),b(β),c(γ)に対して,等式 (1+ i)β-(-1+ i)α=2γが成り立つとき, abc はどのような三角形か。 (2) 異なる3 点o(0),a(α),b(β)に対して,等式α2- αβ+β2=0 が成り立つとき, oab は どのような三角形か。 解答β ¹³⁷Csの場合、余分なエネルギーはβ線および γ線として放出される。 β線は電子、γ線は光子の放射線。 γ あさりよしとお「放射線ってナニモノ?」 放射性核種の基本的性質 ~不安定な原子核~13 Gamma 分布 对Gamma函数做个变形,可以得到如下式子: ∫ 0 ∞ Γ (α) t α − 1 e − t d t = 1 (1 3 1) 取等式左边积分中的函数作为概率密度,就得到一个简单的Gamma分布的密度函数: G a m m a (t ∣ α) = Γ (α) t α − 1 e − t 如果做一个变换 t = β x t=\beta x t = β x ,代
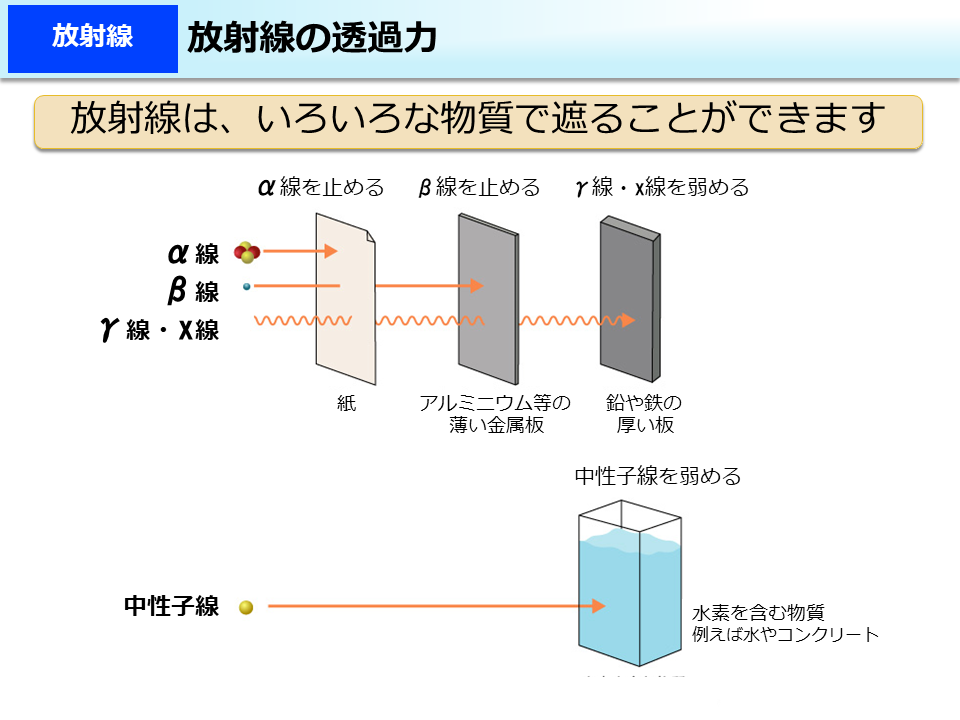



環境省 放射線の透過力




三角関数 の基本的な定理とその有用性を再確認してみませんか その1 正弦定理 余弦定理 正接定理 ニッセイ基礎研究所
1個兩次對稱軸 或 1個對稱面 3 13 2 α=γ=90°,β≠90°,a≠b≠c 單斜 正交/斜方 3個兩次對稱軸 或 1個兩次對稱軸2個對稱面 3 59 4 α=β=γ=90°,a≠b≠c 正交/斜方 四方/正方 1個四次對稱軸 7 68 2 α=β=γ=90°,a=b≠c 四方/正方 六方 三方 1個三次對稱軸 5 7 1 α=β=γ≠90




新型コロナウイルスに関するq A 一般の方向け 厚生労働省




燃料費調整制度 電気 関西電力 個人のお客さま
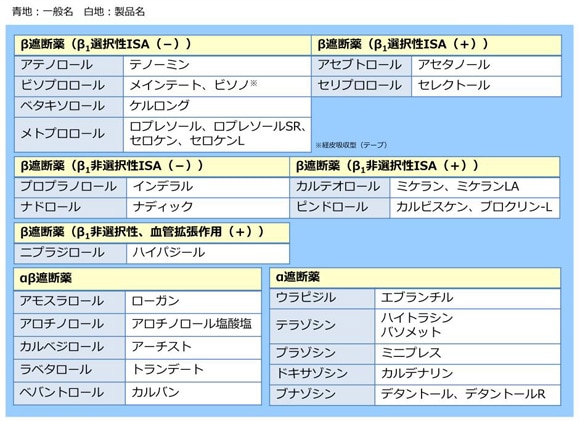



23 B遮断薬 Ab遮断薬 A遮断薬 一覧 基礎から学べる循環器疾患講座 治療編 テキスト解説 薬剤師向け情報 アダラート 製品情報 バイエル ファーマ ナビ




1994 号 カラー映像信号のスムージング回路及び同期信号挿入回路 Astamuse




号 異常検知装置 異常検知方法 および コンピュータプログラム Astamuse




Beta Gamma Sigma オナーズソサエティー 立命館アジア太平洋大学




いまさら聞けないがんの基礎 5 Wnt B カテニン シグナル伝達経路とは Learning At The Bench




どんな問題でもそうなんですが A B Gはこの順番通りなんですか Clearnote




Xperia 1 Ii Xq At42 Xperia Tm スマートフォン ソニー




3次方程式の解と係数の関係 おいしい数学




表層地盤の増幅特性に関して Kke解析技術者ブログ 構造計画研究所



日本白内障学会
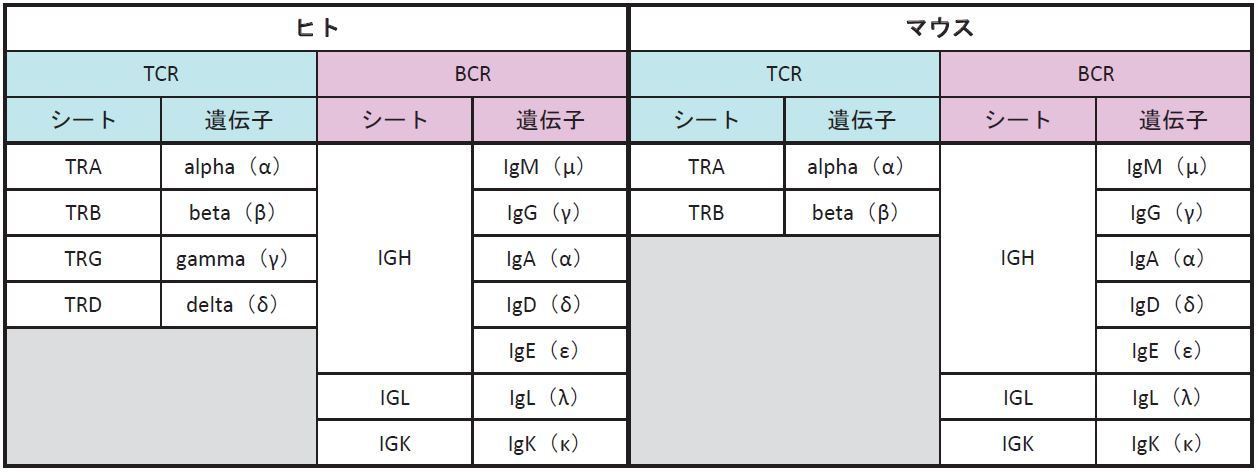



解析データの見方について Tcr r レパトア解析 Repertoire Genesis



イラストでわかる シクロデキストリン 株式会社シクロケム




Whoが変異ウイルスにギリシャ文字の新名称 あらためて知りたい 変異ウイルスの性質 一覧 Business Insider Japan
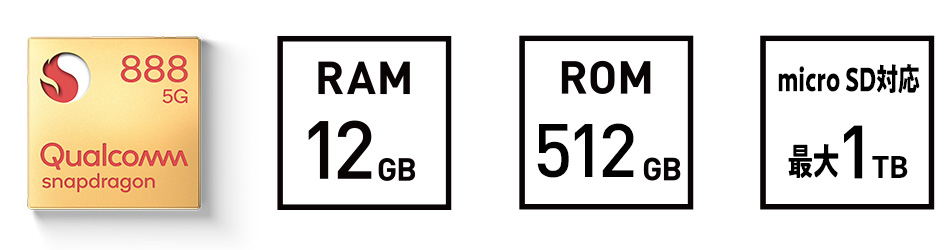



Xperia 1 Iii Xq 42 Xperia Tm スマートフォン ソニー
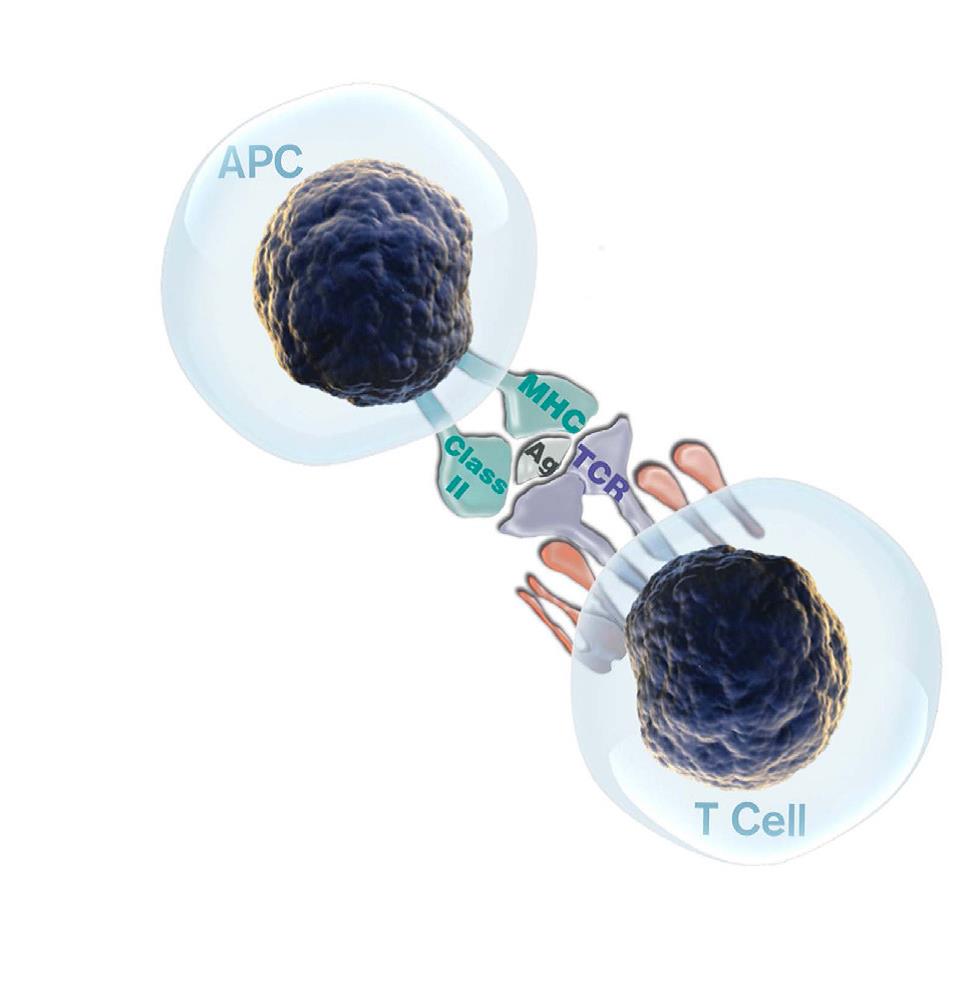



Iotest Beta Mark Tcr Vbレパトワ解析キット サイトメトリードットコム
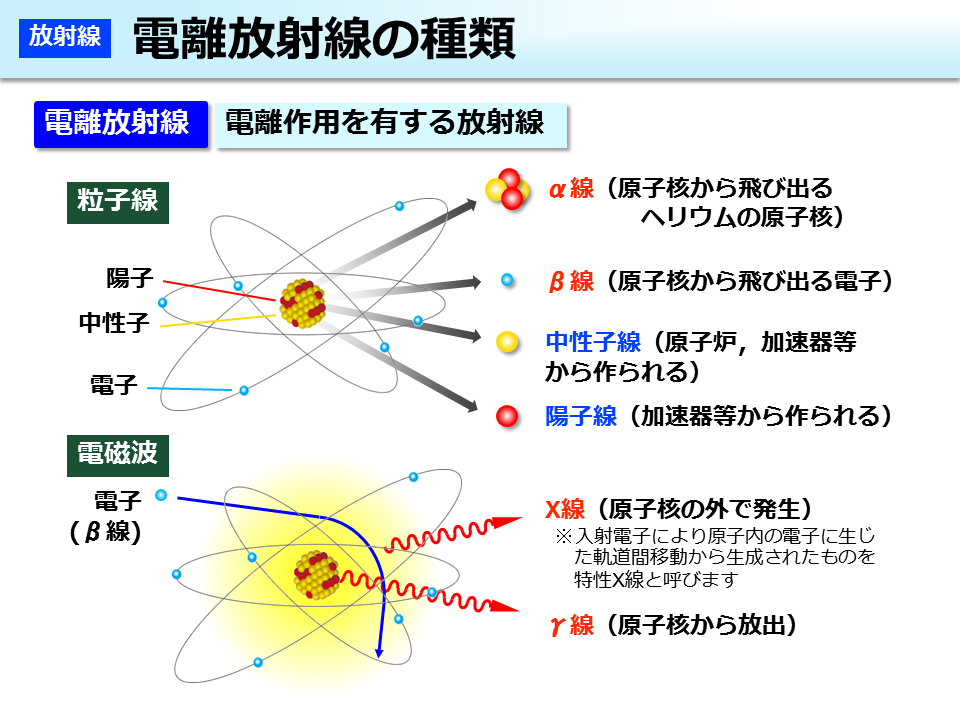



環境省 電離放射線の種類




解と係数の関係は覚えるな 2次でも3次でもすぐに導ける




外部被ばくと内部被ばく 放射線の基礎知識 長瀬ランダウア株式会社



2
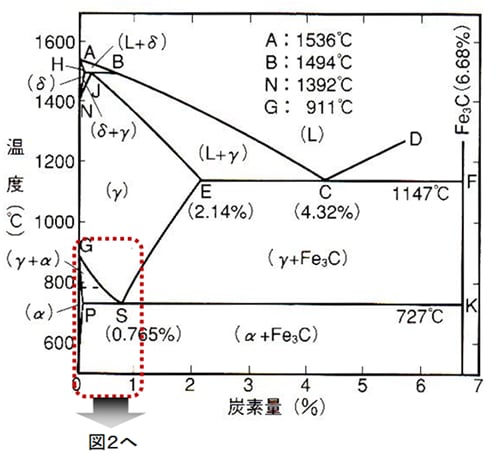



鉄鋼の温度と金属組織の関係 鉄 炭素系平衡状態図 通販モノタロウ



2



2



2




耳と目からのg波の刺激でアルツハイマー原因物質が減る Beyond Health ビヨンドヘルス




22 B遮断薬 A遮断薬 作用機序 基礎から学べる循環器疾患講座 治療編 テキスト解説 薬剤師向け情報 アダラート 製品情報 バイエル ファーマ ナビ



Changing Variables



2




新型コロナ 南米で拡大しているラムダ型変異ウイルス 現時点で分かっていることは 忽那賢志 個人 Yahoo ニュース



大阪府立大学ベンチャー 株式会社michs ミクス Micro Reactor Items




Ysパイル工法 ジオテック株式会社




学科 コース 学園紹介 細田学園高等学校



感覚メディア研究室 Opengl 同次変換の利用と3次元 Pukiwiki



2




Amazon 森博嗣 Gシリーズ 9冊セット F 8 T L H B G ファイ シータ タウ イプシロン ラムダ イータ アルファ ベータ ガンマ おもちゃ おもちゃ
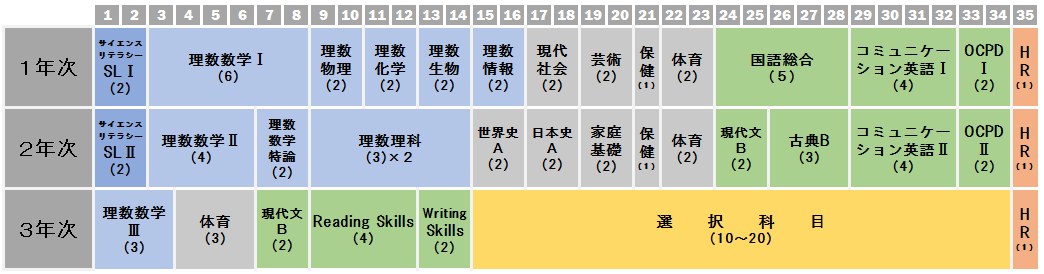



教育課程表 時間割 横浜サイエンスフロンティア高等学校




高校数学b 漸化式を利用する方程式の解の高次対称式a N B N G Nの値 受験の月



Conflex Tutorials



2




7gnuoygmmowsgm




血液の成分は何 看護roo カンゴルー
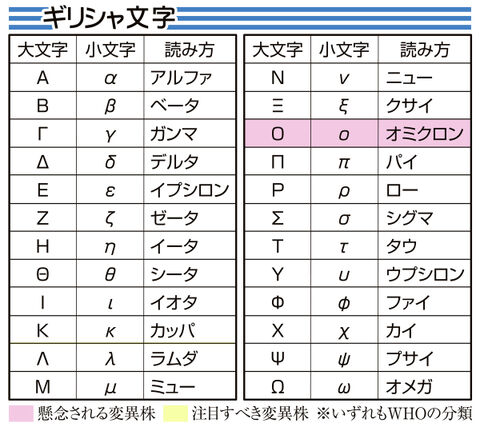



ラムダ ミュー オミクロン 変異株から学ぶギリシャ文字 全24文字のどこまで出現 河北新報オンラインニュース Online News
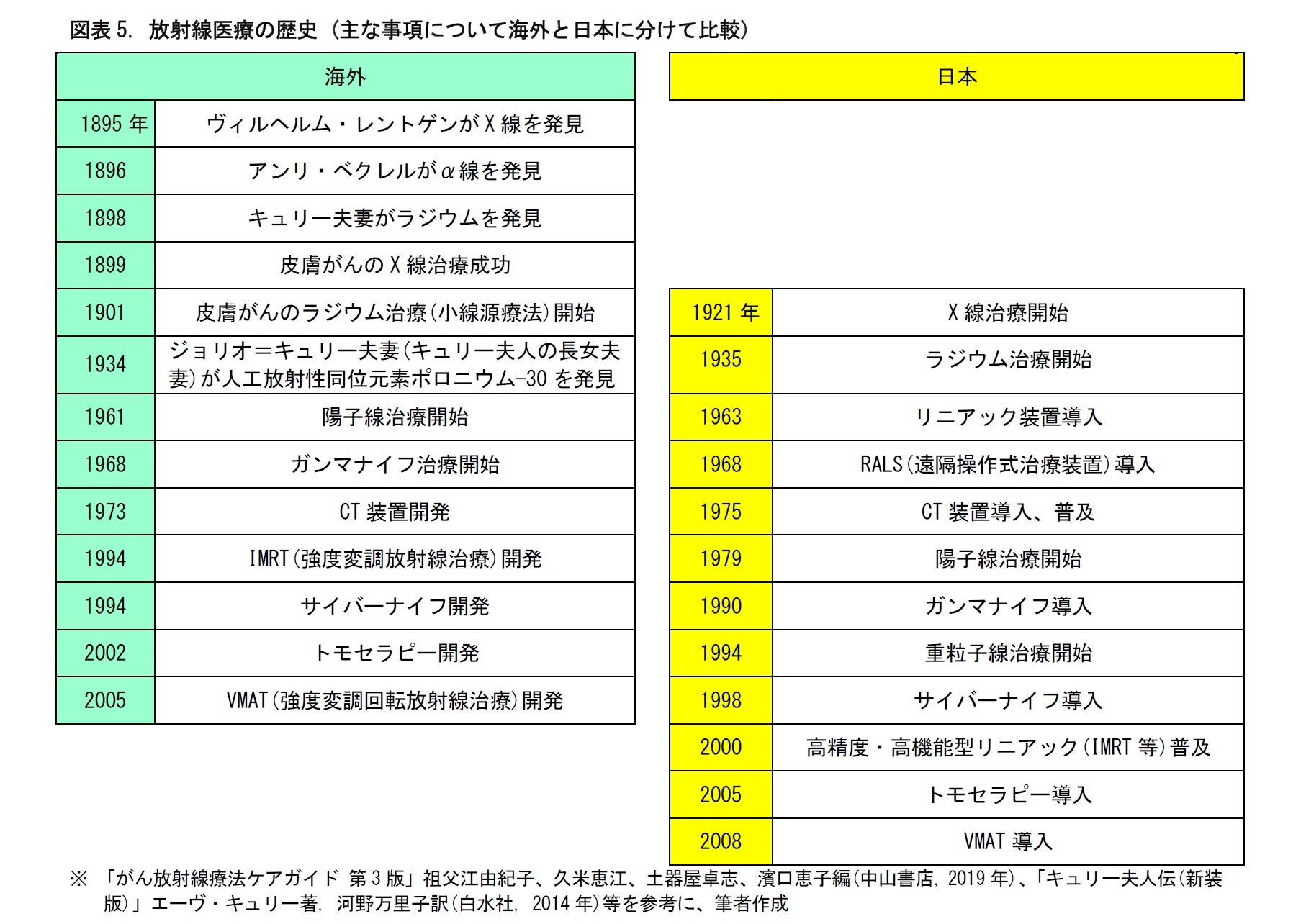



放射線の画像検査への活用 放射線医療の現状 前編 ニッセイ基礎研究所
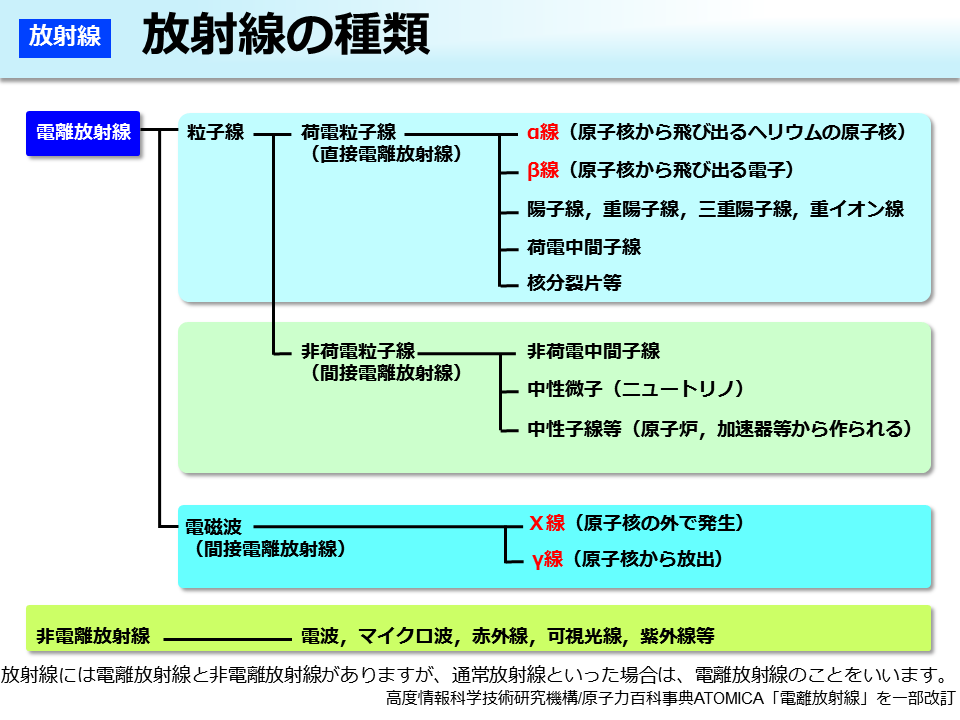



環境省 放射線の種類
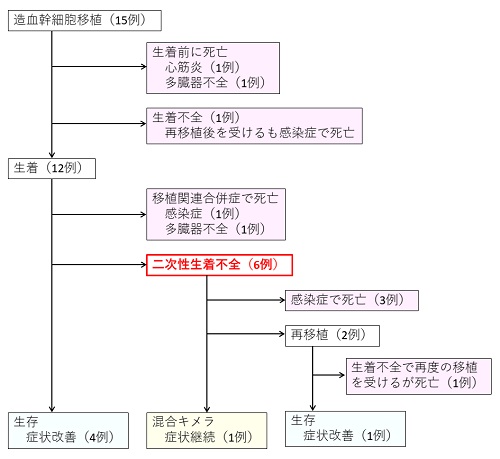



研究成果 まれな原発性免疫不全症に対する造血幹細胞移植の有効性と問題点を解明 広島大学




Anti Integrin Alpha V 抗体 Epr Ab アブカム



2



新型コロナウイルス変異株 デルタ株 について 感染力 潜伏期間 ワクチンの効果 ひまわり医院 内科 皮膚科
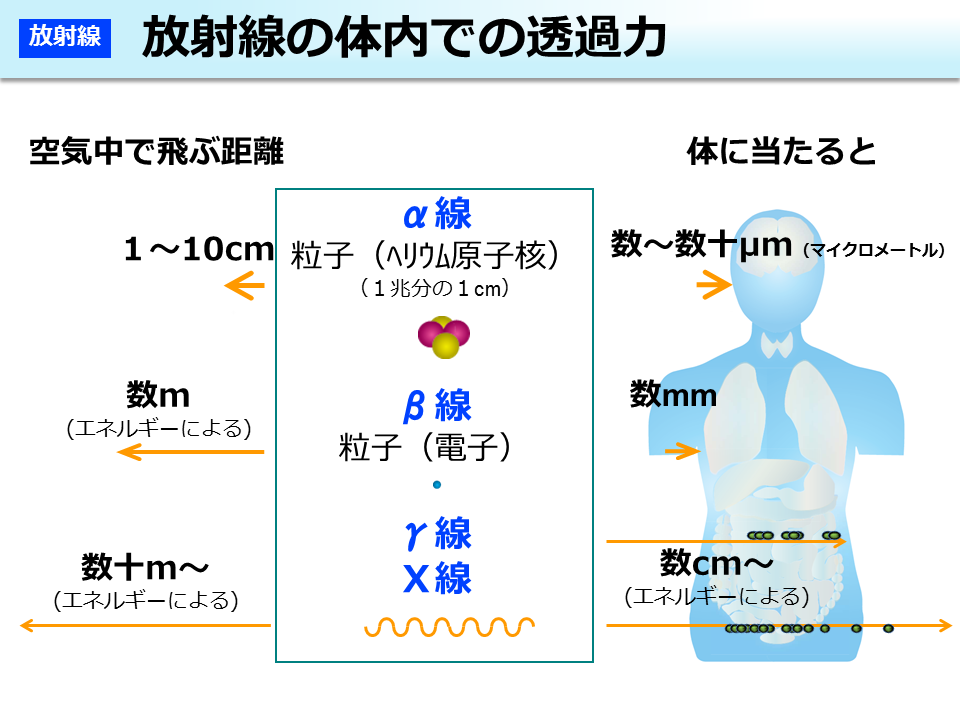



環境省 放射線の体内での透過力




いまさら聞けないがんの基礎 5 Wnt B カテニン シグナル伝達経路とは Learning At The Bench




Xax3c0heeh0ltm



日本白内障学会




4 ユビキタスネットワークの進展と経済成長 平成19年版 情報通信白書
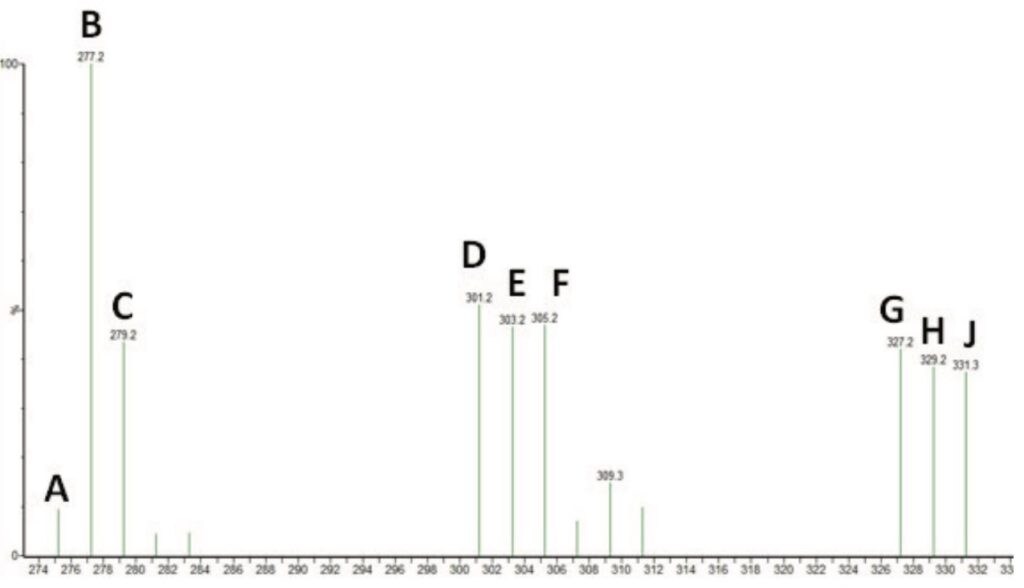



オイルサプリメント中の脂肪酸のアンビエントイオン化 Dart および質量検出による迅速スクリーニング Waters
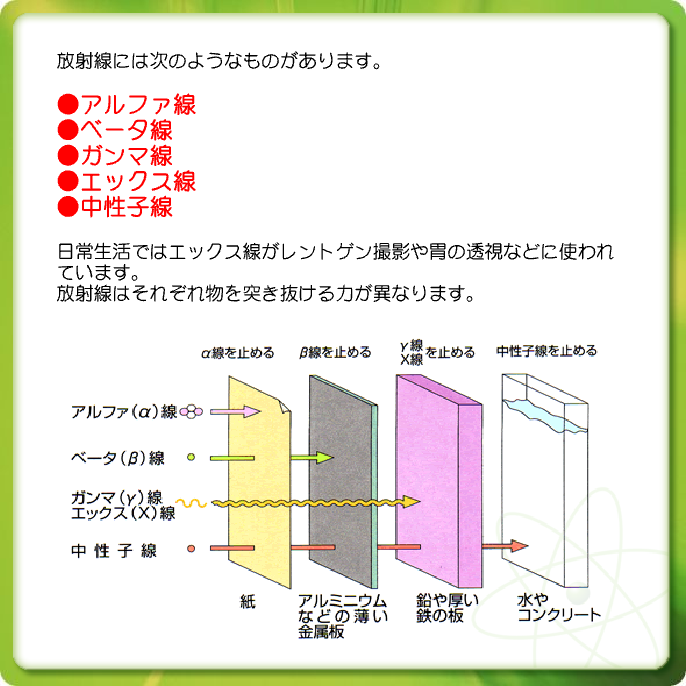



原子力豆知識 東通村と原子力




マンガで学ぶ 医師が教える コロナ変異株 N501y について 株式会社smart119のプレスリリース
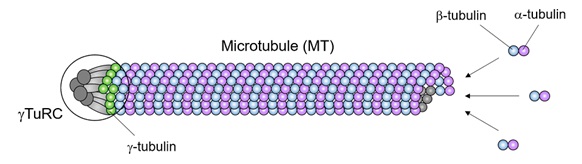



注目の研究分野 細胞分裂 有糸分裂 チューブリン Cell Cycle Mitosis Microtubule Tubulin 細胞周期 微小管研究用製品特集 フナコシ



Opengl勉強会用 資料のページ




アルファ ベータ ガンマ 変異株へのギリシャ文字使用には 理由がある ブログ 菊正宗ネットショップ



2




新型コロナウイルス変異株の名前 ギリシャ文字はあと12個で終了 その後どうなる 朝日新聞globe




耳と目からのg波の刺激でアルツハイマー原因物質が減る Beyond Health ビヨンドヘルス




Whoが変異ウイルスにギリシャ文字の新名称 あらためて知りたい 変異ウイルスの性質 一覧 Business Insider Japan



グローバル特進コース A B 学校法人大阪初芝学園 初芝立命館中学校 高等学校




Ocn V6アルファ Nttコミュニケーションズ 個人のお客さま
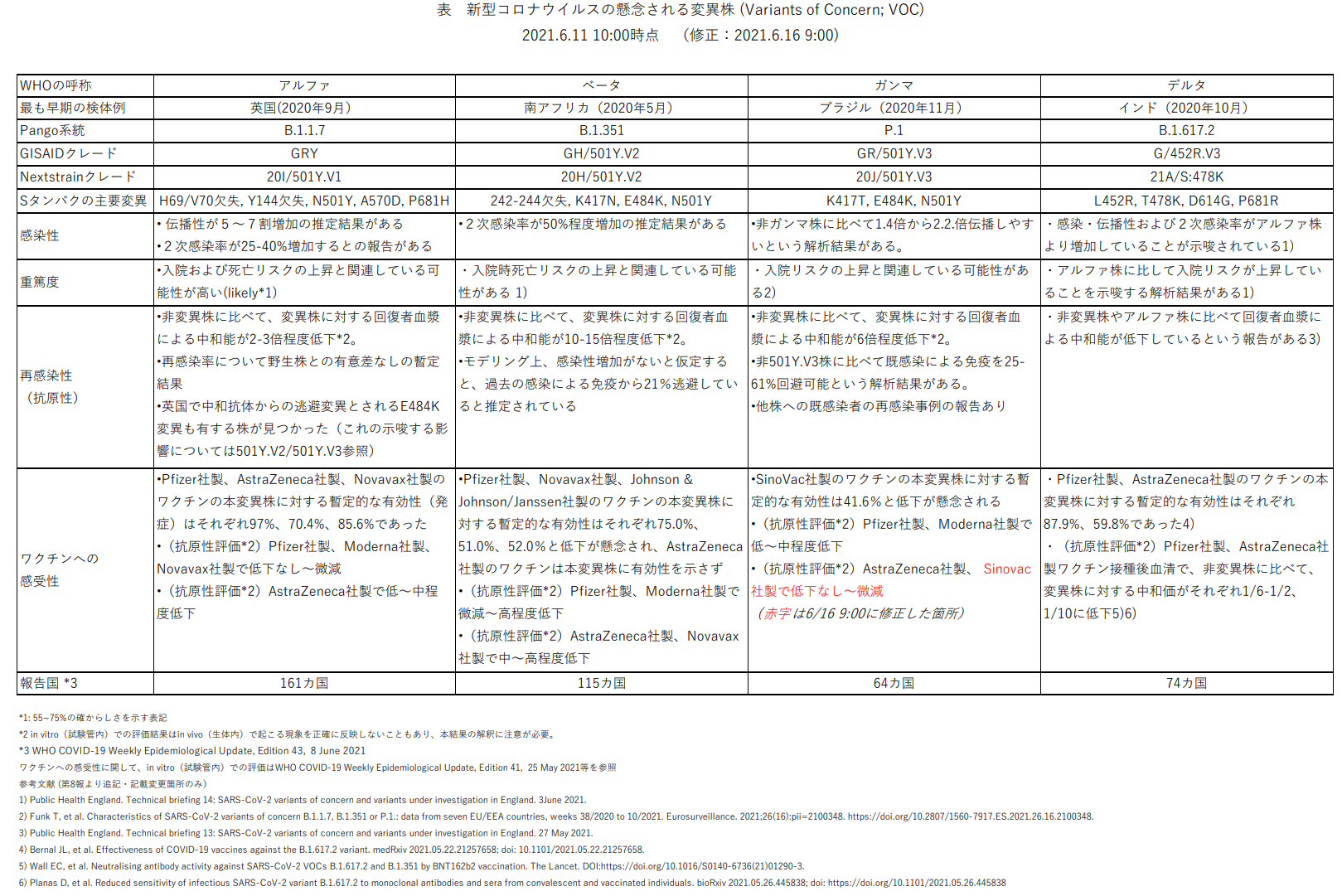



感染 伝播性の増加や抗原性の変化が懸念される 新型コロナウイルス Sars Cov 2 の新規変異株について 第9報




慶應義塾湘南藤沢中等部 高等部公式サイト 教育 未来を創り出す力 各教科の紹介
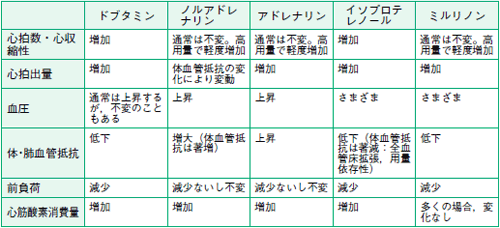



強心薬 昇圧薬の使いかた 2 大野博司 10年 記事一覧 医学界新聞 医学書院



2




三次方程式の解と係数の関係では 3つの解をa B G とすると Ax Bx Clearnote




Whoが変異ウイルスにギリシャ文字の新名称 あらためて知りたい 変異ウイルスの性質 一覧 Business Insider Japan
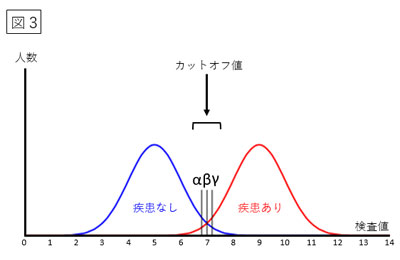



感度と特異度の視覚的理解 札幌西円山病院リハビリテーションセンター Blog
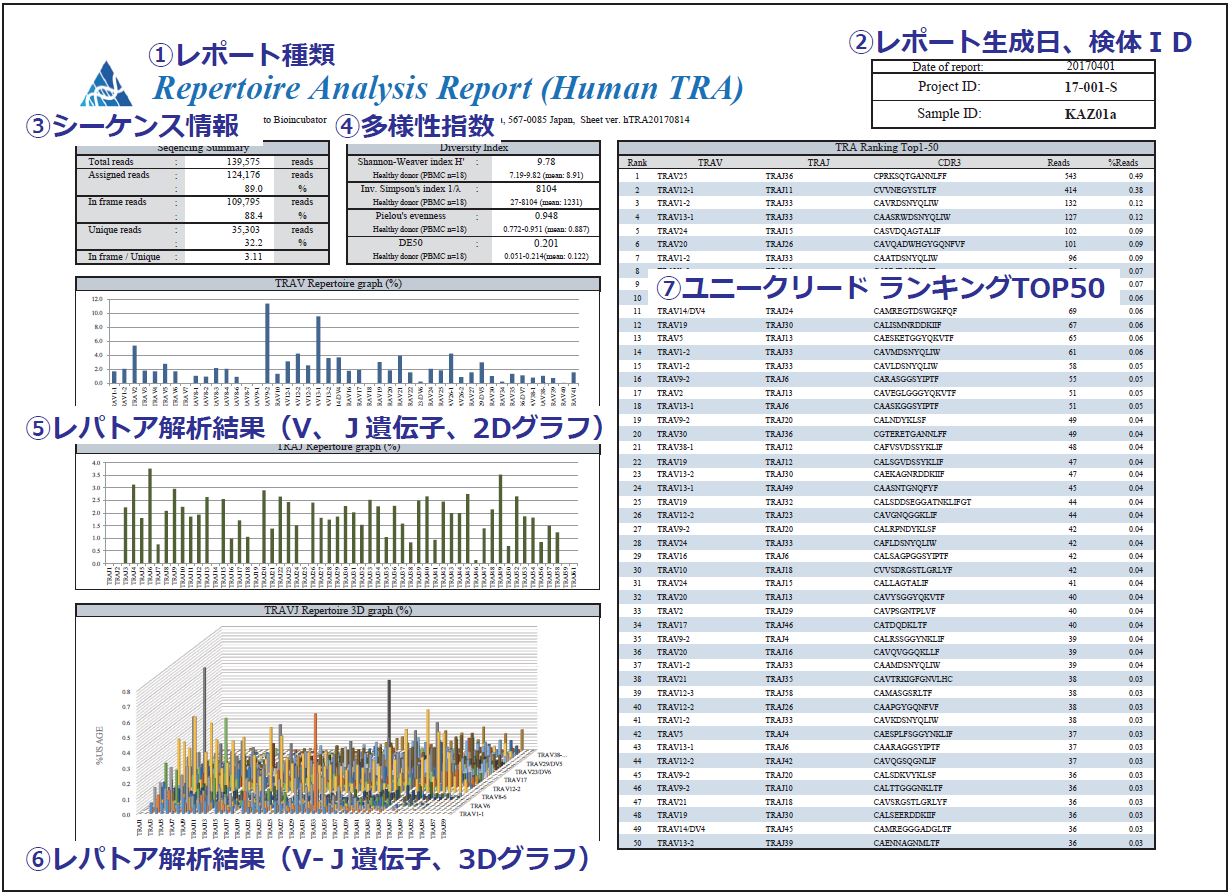



解析データの見方について Tcr r レパトア解析 Repertoire Genesis
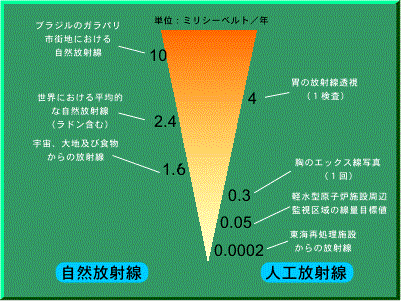



環境放射線モニタリング情報




燃料費調整制度 電気 関西電力 個人のお客さま




カリキュラム 早稲田大学 データ科学センター




鉄則7 方程式 3次方程式と3根 寺田の数学合格鉄則96に関するメモ




マンガで学ぶ 医師が教える コロナ変異株 N501y について 株式会社smart119のプレスリリース
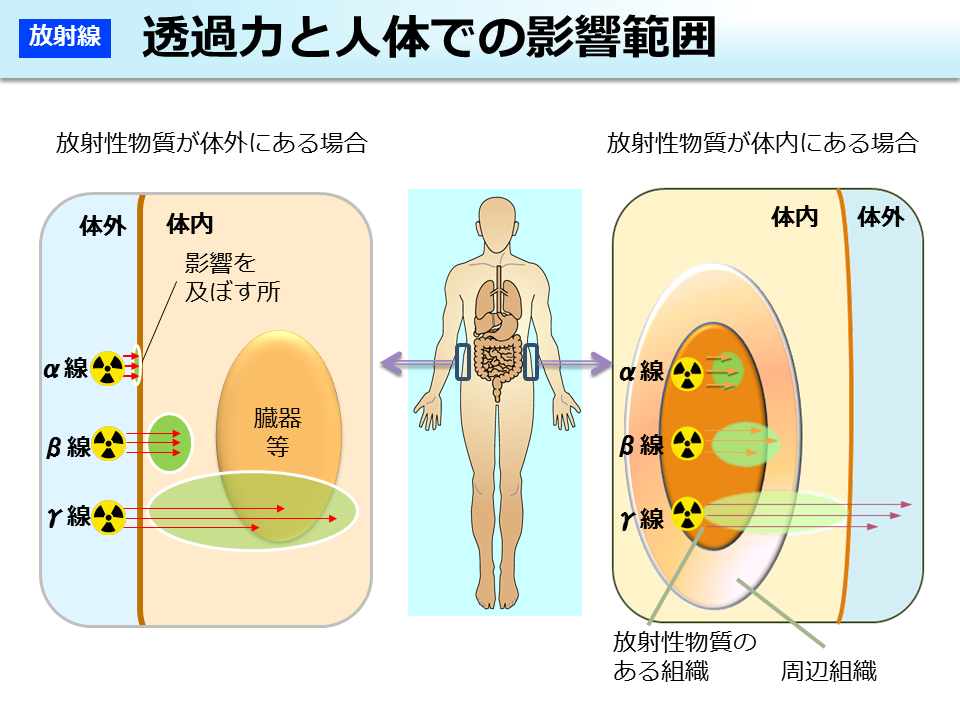



環境省 透過力と人体での影響範囲
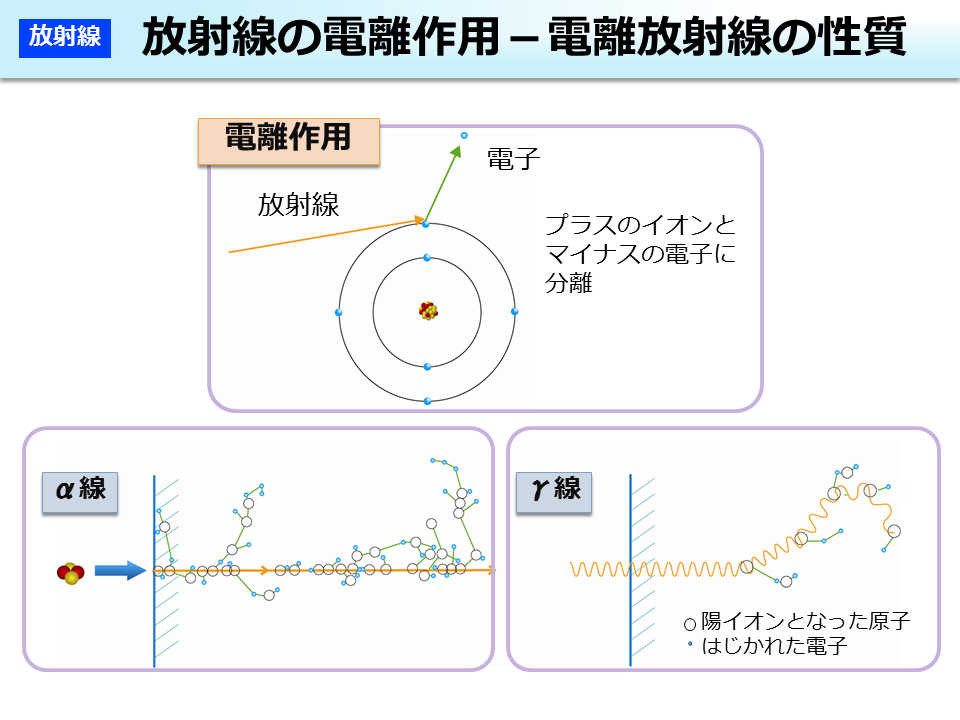



環境省 放射線の電離作用 電離放射線の性質




00 号 二次電池の電池容量劣化算出方法 Astamuse




変異株に新名称 アルファ デルタなど 新型コロナ ミニ知識




いまこそ知っておくべき コロナウイルス に関する4つの基礎知識 Wired Jp
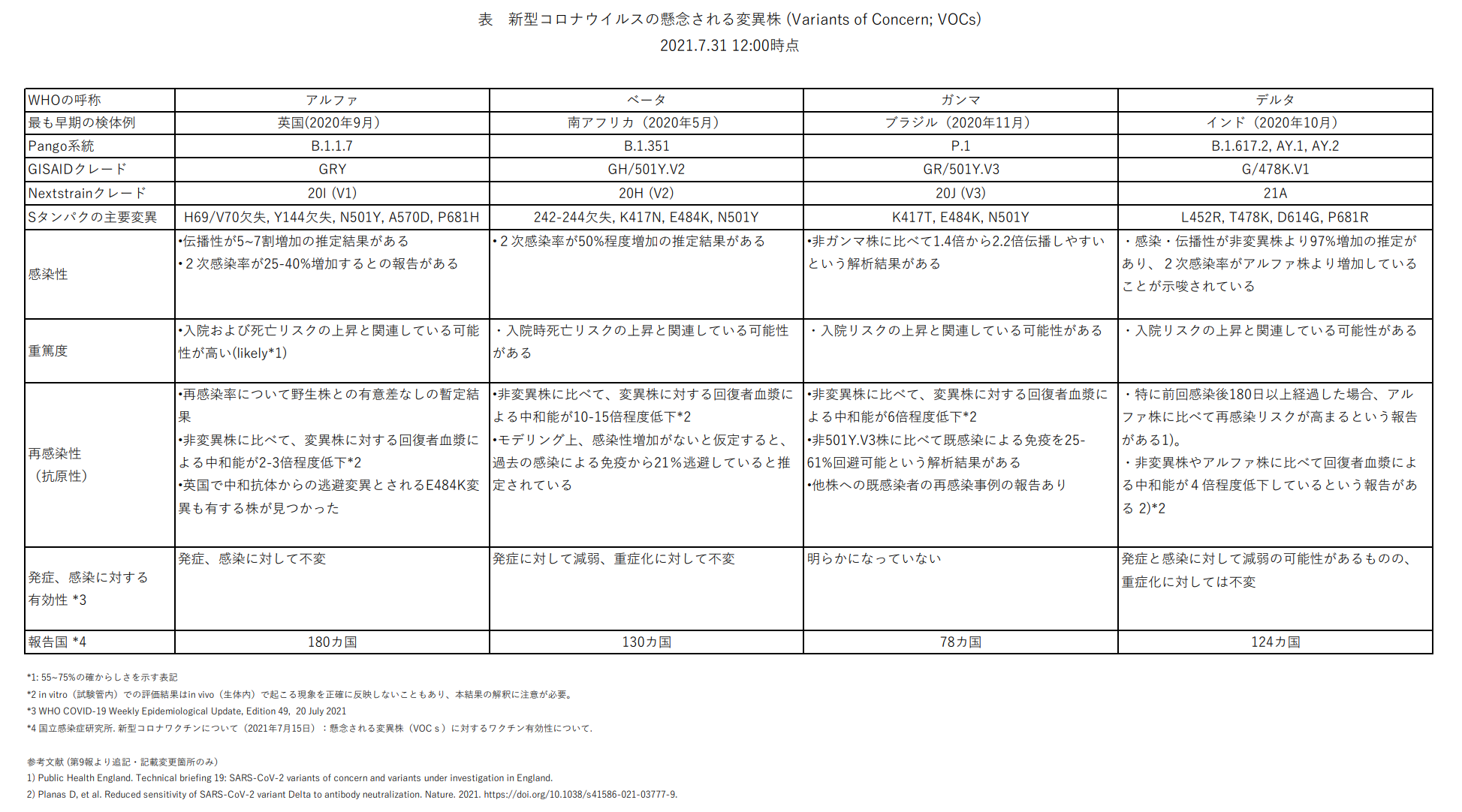



感染 伝播性の増加や抗原性の変化が懸念される 新型コロナウイルス Sars Cov 2 の新規変異株について 第12報



2



2




根と係数の関係 Wikipedia



0 件のコメント:
コメントを投稿